Thingiverse

Irregular Tesselating Pentagon Type 6 by claudeShannon
by Thingiverse
Last crawled date: 3 years, 4 months ago
Irregular Tesselating Pentagon Type 6
John Matz
11/13/2020
George Mason University
Math 401: Mathematics Through 3D Printing
This irregular pentagon is one of the fifteen pentagons that can seamlessly tile the infinite plane. Though this particular tile is concave or nonconvex, it is a type 6 pentagon, which is one of the pentagons that will tessellate as either a convex or concave type. According to Wikipedia, “Types 1, 2, 4, 5, 6, 7, 8, 9, and 13 allow parametric possibilities with nonconvex prototiles.”[1]
The Type 6 pentagon is one of three pentagon types (6, 7 & 8) discovered by Richard Kershner in 1968.[1] He believed that these were the last possible pentagonal tilings, but seven more types were subsequently discovered.[1] Only recently, in July 2017, did Michaël Rao successfully execute a computer-assisted proof that demonstrated that there were no remaining undiscovered convex pentagonal tile types.[1]
The Type 6 pentagon is differentiated from other pentagonal tiles by its conformity to five apparently simple equations[1]:
a = d = e (1)
b = c (3)
B + D = 180° (4)
2B = E (5)
When the internal angle A is greater than 180° the pentagon becomes concave, as mine is. I gained a better understanding of the underlying geometry of this pentagon by dividing it into three triangles and attempting to solve for all of the sides and angles. According to Quanta Magazine, all n-gons are divisible into n-2 triangles, thus all pentagons are divisible into 3 triangles.[2] Defining angle B as 19°, D is then 161° by equation (4), and E is 38° by equation (5). Then, by defining one of the component triangles at that adjacent to point E, it is clear that triangle must be isosceles and it is possible to find the other two angles of this triangle. Starting from this basis, it is possible to solve for all the other angles and side lengths by hand through use of the Law of Sines, the Law of Cosines, and basic trigonometry.
[1] https://en.wikipedia.org/wiki/Pentagonal_tiling
[2] https://www.quantamagazine.org/the-math-problem-with-pentagons-20171211/
John Matz
11/13/2020
George Mason University
Math 401: Mathematics Through 3D Printing
This irregular pentagon is one of the fifteen pentagons that can seamlessly tile the infinite plane. Though this particular tile is concave or nonconvex, it is a type 6 pentagon, which is one of the pentagons that will tessellate as either a convex or concave type. According to Wikipedia, “Types 1, 2, 4, 5, 6, 7, 8, 9, and 13 allow parametric possibilities with nonconvex prototiles.”[1]
The Type 6 pentagon is one of three pentagon types (6, 7 & 8) discovered by Richard Kershner in 1968.[1] He believed that these were the last possible pentagonal tilings, but seven more types were subsequently discovered.[1] Only recently, in July 2017, did Michaël Rao successfully execute a computer-assisted proof that demonstrated that there were no remaining undiscovered convex pentagonal tile types.[1]
The Type 6 pentagon is differentiated from other pentagonal tiles by its conformity to five apparently simple equations[1]:
a = d = e (1)
b = c (3)
B + D = 180° (4)
2B = E (5)
When the internal angle A is greater than 180° the pentagon becomes concave, as mine is. I gained a better understanding of the underlying geometry of this pentagon by dividing it into three triangles and attempting to solve for all of the sides and angles. According to Quanta Magazine, all n-gons are divisible into n-2 triangles, thus all pentagons are divisible into 3 triangles.[2] Defining angle B as 19°, D is then 161° by equation (4), and E is 38° by equation (5). Then, by defining one of the component triangles at that adjacent to point E, it is clear that triangle must be isosceles and it is possible to find the other two angles of this triangle. Starting from this basis, it is possible to solve for all the other angles and side lengths by hand through use of the Law of Sines, the Law of Cosines, and basic trigonometry.
[1] https://en.wikipedia.org/wiki/Pentagonal_tiling
[2] https://www.quantamagazine.org/the-math-problem-with-pentagons-20171211/
Similar models
grabcad
free

Pentagonal tiling
...pentagonal tiling
grabcad
the 15th monohedral convex pentagonal type, discovered in 2015
thingiverse
free

Pentomizer - Every known tessellating convex pentagon by mathgrrl
...just one pentagon, or might include infinitely many somewhat similarlooking pentagons. "only this year" means that this year, after...
3dwarehouse
free

Floret Geodesic Tessellation
...gonal tiling, at wikipedia: #buckminster #bucky #buckyball #dome #fuller #geodesic #icosahedron #polyhedron #tessellation #tiling
thingiverse
free

Law of Sines - Teaching manipulative by ZombieCat
... show the same angle a but using the blue tape mark at 8 there can be two different triangles with the same angle a and length a.
thingiverse
free

Quasicrystal by Leiutaja
... to demonstrate and solve the problem of infinite tiling without rhombic gaps between tiles while irregular voids are prohibited.
grabcad
free

15 pentagons which can form a tiled plane.
...can vary shape in their system.
see https://www.zmescience.com/science/math/pentagonal-tile-mathematics-29092017/ for more info.
3dwarehouse
free
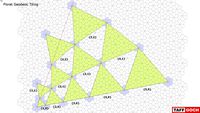
Floret Geodesic Tiling • Map
...tiling, at wikipedia: #buckminster #bucky #buckyball #dome #fuller #geodesic #icosahedron #polyhedron #snub #tessellation #tiling
thingiverse
free

Dromedary tessellation tiles by teunKeusters
... defined by heesch and kienzle.
for printing i recommend using the file with margins, otherwise the tiles probably won't fit.
thingiverse
free

Tessellation of an Equilateral Pentagon by lgbu
...gonal caddy, and a hexagonal caddy. the edge length of a pentagon is 25 mm. it is 3.6 mm in thickness. the caddy is 60 mm tall.
3dwarehouse
free

Geodesic Floret Tessellation
...gonal tiling, at wikipedia: #buckminster #bucky #buckyball #dome #fuller #geodesic #icosahedron #polyhedron #tessellation #tiling
Claudeshannon
thingiverse
free

Test 123 by claudeShannon
...j_a4_stl.stl",a3]
references:
[1] http://www.isc.meiji.ac.jp/~kokichis/reflexivelyfusedobjects/reflexivelyfusedobjectse.html
thingiverse
free

Impossible Pentagon by claudeShannon
...j_a4_stl.stl",a3]
references:
[1] http://www.isc.meiji.ac.jp/~kokichis/reflexivelyfusedobjects/reflexivelyfusedobjectse.html
thingiverse
free

Transfer (Gain) Function for AC Circuit by claudeShannon
...t. also included is my mathematica code, which was based on code given to me by my instructor in mathematics through 3d printing.
Tesselating
turbosquid
$10

Voronoi Tessellation 13
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$10

Voronoi Tessellation 08
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$5

Voronoi Tessellation 01
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$20

Tessellate Nerita Sea Shell
...te nerita sea shell for download as blend, obj, fbx, and gltf on turbosquid: 3d models for games, architecture, videos. (1627589)
turbosquid
$20

Tessellate Nerita Sea Shell
...te nerita sea shell for download as blend, obj, fbx, and gltf on turbosquid: 3d models for games, architecture, videos. (1627588)
3d_export
$69

Walkie Talkie 2 3D Model
...s highly tesselated within the edit poly (not visible in viewport)it uses vray displacement to displace the details in the front.
3d_export
$10
tophelm
...bake and final textures) png, spp<br>thank you for reading to the end, you can comment and like the model, do not forget)).
3d_export
$19

viking two handed axe
...bake and final textures) png, spp<br>thank you for reading to the end, you can comment and like the model, do not forget)).
3d_export
$7

spiral urn and bench
...20_2k_color 2048x2048 - marble020_2k_displacement 2048x2048 - marble020_2k_normal 2048x2048 - marble020_2k_roughness 2048x2048
3d_export
$25

Mushroomhouse subdivision and low poly
...ight (also vray sperical light) as lighting for the renderings. two exr images for the dome light are included with the download.
Pentagon
turbosquid
$25

Pentagon
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$25

Pentagon
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
3d_export
$5

pentagon sphere
...n sphere
3dexport
it is a sphere with a pentagon structure. it is a variant of a triangle sphere which is used in geodesic dome.
design_connected
$13

Le Pentagone
...le pentagone
designconnected
south hill home le pentagone computer generated 3d model. designed by browning, jonathan.
design_connected
$9

Pentagon pouf
...pentagon pouf
designconnected
quinze & milan pentagon pouf poufs computer generated 3d model. designed by thomas tritsch .
3ddd
$1

KARE Mirror Pentagon
...kare mirror pentagon
3ddd
kare
зеркало kare mirror pentagon 110x84cm
turbosquid
$39

PENTAGON CHAIR
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$2

Pentagonal Spaceship
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$3

Pentagon washbasin
...on washbasin for download as 3ds, max, dxf, obj, fbx, and 3dm on turbosquid: 3d models for games, architecture, videos. (1187318)
turbosquid
$10

pentagon coffee table
...ee 3d model pentagon coffee table for download as max and 3ds on turbosquid: 3d models for games, architecture, videos. (1621347)
Irregular
3d_ocean
$3

plant_01
...plant_01 3docean high resolution irregular trunk isolated leaves plant transparent tropical tropical, leafy, plant...
3d_ocean
$6

Funky House
...house playful tiny whimsical a funky 3d house with irregular but fun...
3d_export
free

sofaboxplayswedese
...is robust and elegant at the same time. the irregular shape adds playfulness, and this sofa, straight or corner,...
3d_ocean
$7

Armchair SLOORP
...comfort. casual upholstery with nicely pleaded seams. strong, even irregular formation of creases is...
3d_export
$5

Gray Blue Stone- Rocks 3D Model
...stone blue gray rocks tileable texture diffuse cracks uneven irregular png jpg tga game movie stylized semi-realistic cartoon gray...
3ddd
$1

Iron Rolling Cabinet Locker Console
...cast iron hardware. rivet details, weathered paint and an irregular surface add to its vintage look, creating the appearance...
3ddd
$1

Mirror
...sculptural mirror – the mirror area is framed by irregular reflecting elements superimposed on one another. these are reminiscent...
3d_export
$10

TANKER TRUCK GAME READY 3D MODEL
...century is the improvised fighting vehicle, often seen in irregular warfare.<br>files units are centimeters and the model is accurately...
3d_export
$5

MILITARY TANKER VEHICLE MODEL GAME READY
...century is the improvised fighting vehicle, often seen in irregular warfare.<br>files units are centimeters and the model is accurately...
thingiverse
free
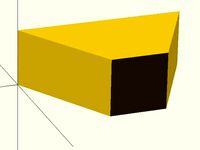
Irregular Frustum by 63alfred
...irregular frustum by 63alfred
thingiverse
openscad model of irregular frustum
Type
3d_export
$5

s type
...s type
3dexport
s type formats max 3ds obj stl
3d_export
$5
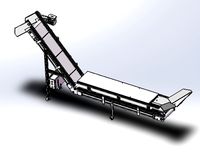
l-type conveyor
...l-type conveyor
3dexport
l-type conveyor
3d_export
$5

volkswagen type 2
...volkswagen type 2
3dexport
volkswagen type 2
turbosquid
$150

RBC types
...osquid
royalty free 3d model rbc types for download as blend on turbosquid: 3d models for games, architecture, videos. (1343563)
turbosquid
$1

B-Type
...urbosquid
royalty free 3d model b-type for download as blend on turbosquid: 3d models for games, architecture, videos. (1609608)
3ddd
$1

shoes type A
...shoes type a
3ddd
туфли
shoes
turbosquid
$39

R-type
...oyalty free 3d model r-type for download as max, obj, and fbx on turbosquid: 3d models for games, architecture, videos. (1303675)
turbosquid
$5

melon type
...ee 3d model melon galia type for download as ma, fbx, and obj on turbosquid: 3d models for games, architecture, videos. (1557188)
3d_export
free

three different type
...three different type
3dexport
three different type: mace, axe, sword
turbosquid
$49

Types of Placentation
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
6
3d_export
$18

tulip 6
...tulip 6
3dexport
tulip 6
3d_export
$5

hinge 6
...hinge 6
3dexport
hinge 6
3ddd
$1

MASIERO / FLASHWOOD STL 6 + 6
...6
3ddd
masiero
торшер flashwood stl 6 + 6 фабрики masiero
http://www.masierogroup.com/c87_697/it/flashwood%20stl%206%20+%206.ashx
turbosquid
$110

Atmos Cannon 2000 6*6
...yalty free 3d model atmos cannon 2000 6*6 for download as skp on turbosquid: 3d models for games, architecture, videos. (1528591)
turbosquid
$1

ae 6 6 electric locomotive
... free 3d model ae 6 6 electric locomotive for download as obj on turbosquid: 3d models for games, architecture, videos. (1707537)
turbosquid
$39

A-6
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
3ddd
$1

6 ковров
...6 ковров
3ddd
ковры , ковер
6 ковров
turbosquid
$12

Calligraphic Digit 6 Number 6
...hic digit 6 number 6 for download as max, obj, fbx, and blend on turbosquid: 3d models for games, architecture, videos. (1389336)
turbosquid
$19

Case For Phone 6 Girl 6
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
turbosquid
$35

Iphone 6 & 6 Plus All
... available on turbo squid, the world's leading provider of digital 3d models for visualization, films, television, and games.
